Top | Criticism | Alternative | Miscellaneous | Bottom
Eric Lerner starts his book "The Big Bang Never Happened" (hereafter BBNH) with the "errors" that he thinks invalidate the Big Bang. These are
Are these criticisms correct? No, and they were known to be incorrect in 1991 when Lerner wrote his book.
Let us look at the superclusters first.
Lerner gives the example of filaments or sheets 150 million light years apart in Figure 1.1, and then asserts that material would have to travel 270 million light years to make the structure. Obviously 75 million light years would do the trick. With material traveling at 1000 km/sec, that would take 22.5 billion years, which is about twice as long as the probable age of the Universe. But when the Universe was younger, everything was closer together, so a small motion made early in the history of the Universe counts for much more than a motion made later. Thus it was easier for the material to clump together early in the history of the Universe. Lerner's math here is like ignoring interest when planning for retirement. If you save $1000 per year for 50 years, you don't retire with $50,000. If the interest rate was 7 percent throughout the 50 years, you will have a $460,000 nest egg.
Furthermore, velocities relative to the Hubble flow naturally decrease with time, so the 1000 km/sec velocity was larger in the past. Lerner's discussion of this point uses loaded words and incorrect logic. He quotes unnamed cosmologists as "speculating" that matter moved faster in the past, and calls this an "unknown" process. In fact, it is just Newton's First Law. Consider an object moving at 1000 km/sec relative to the Hubble flow at our location. For Ho = 65 km/sec/Mpc this object will have moved 1.54 Mpc in 1.5 Gyr, the time it takes for the Universe to grow by 10% for this value of Ho. Its velocity will still be 1000 km/sec, but the Hubble flow at a distance of 1.54 Mpc is 1.54*65 = 100 km/sec, so the object's velocity relative to the Hubble flow is now only 900 km/sec. It went down by 10% while the Universe grew by 10%.
For example, the neutrinos in the hot dark matter model are just coasting, or "free streaming". If a free streaming neutrino has 1000 km/sec velocity now, then since recombination it has traveled from a point that is now 2.8 billion light years away. If instead of free streaming the material has been accelerated by gravitational forces, then the relation between velocity relative to the Hubble flow and the distance to the starting point (measured now), is
v = H*D*Omega0.6Using Lerner's value of 1000 km/sec, and a distance of 75 million light years, and Ho = 50 km/sec/Mpc, we find perfect agreement as long as Omega is close to 1. So Lerner's "structures that take too long to grow" are just more evidence for a large amount of dark matter.
In fact, Jim Peebles at Princeton had calculated just how much inhomogeneity in the early Universe would have been needed to grow into the large scale structures we see today. The anisotropy can be used to measure the inhomogeneity. This calculation was published in 1982 (ApJ Lett, 263, L1) and showed that an anisotropy of the temperature of the microwave background with an RMS quadrupole amplitude of 6 microKelvin would have been produced by the inhomogeneity necessary to produce the clustering of galaxies, if the Hubble constant was Ho = 100 km/sec/Mpc. For Ho = 50, the RMS quadrupole would be 12 microK. The actual limit at the time was 600 microK, so there wasn't any problem producing the large scale structure. Later results reduced the limit on the RMS quadrupole to 200 microK by the time Lerner published his book. Thus when Lerner wrote the BBNH, models could reproduce the observed large scale structure with initial conditions that were twenty times more uniform than the observed limit on homogeneity.
In 1991 the limit was reduced to 22 microK by the FIRS balloon experiment and then COBE discovered the anisotropy with a level of 17+/- 5 microK and the current best value is 18.4+/-1.6 microK.
So where was the "crisis"? The "crisis" only arises if there is no dark matter. Without dark matter you need 10 times larger initial perturbations and thus a 10 times larger RMS quadrupole, which was finally ruled out in 1991 after Lerner wrote his book.
Lerner quotes George Field saying there was a crisis, but doesn't give a citation in the book. I remember many newspaper articles saying there was a crisis, but those of us building the COBE satellite knew that nobody had made observations with enough sensitivity to test the models calculated by Peebles, and just hoped that COBE would work well enough to do the job.
By 1992, the model Peebles used had been named "Cold Dark Matter" and people were saying it was "dead" (see "The End of Cold Dark Matter?" by Davis et al., 1992, Nature, 356, 489). But this was from trying to get the details just right: you could make the superclusters and then you had too many cluster of galaxies, or you could make the clusters with a smaller RMS quadrupole and then made too few superclusters. The COBE measurement matched the value needed to make the superclusters. Thus the problem with CDM is that it makes too much structure, not too little. There are several ways to modify CDM to make it work:
Ironically, while Lerner uses this false argument against the Big Bang to advocate an infinitely old Universe, young Earth creationists use the same argument to bolster their belief that the Universe is only several thousand years old.
There is certainly lots of evidence for dark matter. When one looks at cluster of galaxies, the gravitational effects of the cluster can be measured three ways. One is by the orbital motions of the galaxies in the cluster. This was first done by Zwicky in 1933 (Helv. Phys. Acta, 6, 110)! A second looks at the hot gas trapped in many big clusters of galaxies. The third way looks at the bending of light from galaxies behind the cluster by the mass in the cluster (gravitational lensing). All three methods give masses that appear to be very much larger than the mass of the stars in the galaxies in the cluster. This is usually given as the mass-to-light ratio, and M/L is several hundred solar units for clusters of galaxies and only about 3 for the stars in the Milky Way near the Sun.
The paper that Lerner cites as evidence for a lack of dark matter, Valtonen and Byrd (1986, ApJ, 303, 523), claims that the Coma cluster of galaxies and the other great clusters of galaxies are not bound objects. However, the observed velocities within the cluster would cause them to disperse in much less than the age of the Universe, so this claim is quite strange. Furthermore, the X-ray and gravitational lensing evidence now available show that Valtonen and Byrd were incorrect.
The only way to satisfy these observations without a lot of dark matter is to hypothesize that the force of gravity is much stronger at large distances than Newton (or Einstein) would predict. This model is called MOND, for Modification Of Newtonian Dynamics, and it has some adherents. But no good relativistic version of MOND exists, and the existence of gravitational lensing in cluster of galaxies requires a relativistic theory that makes the same change for light and for slow moving objects like galaxies. Furthermore, if the MACHO results hold up, then the MOND model will fail for the halo of the Milky Way. If we then need dark matter to explain the Milky Way halo, it is most reasonable to use the same explanation in distant clusters of galaxies.
More about dark matter.
Lerner claims that the CMB spectrum presented by Mather in 1990 was "too perfect", and that it made it impossible for large scale structure to be formed. However, the perfect fit to the blackbody only ruled out explosive structure formation scenarios like the Ostriker and Cowie model (1981, ApJL, 243, L127). The limits on distortion of the CMB spectrum away from a blackbody are now about 100 times better, and these tighter limits are easily met by models which form large scale structure by gravitational perturbations acting on dark matter. Models which act via electromagnetic interactions, like the explosive structure formation scenario or the plasma Universe have a much harder time meeting the constraints imposed by the FIRAS observations of the CMB spectrum.
Top | Criticism | Alternative | Miscellaneous | Bottom
What alternative does Lerner give for the Big Bang? Since the Big Bang is based on
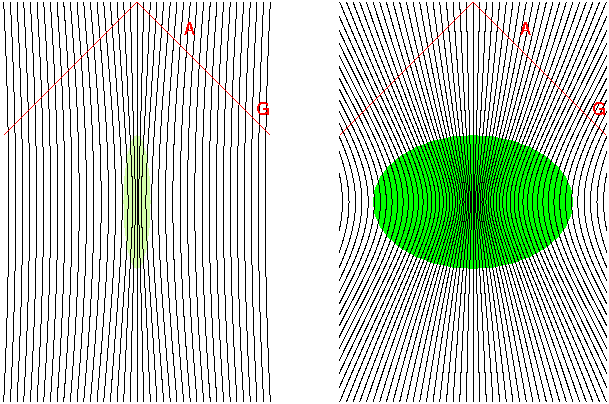
In the BBNH, Lerner presents the Alfven-Klein model which explains the redshift using a portion of the Universe that starts to collapse, then the collapse is reversed. This model requires new physics to generate the force necessary reverse the collapse Figure 6.2 of BBNH shows the collapse, reversal, and later expansion of a region of space. The figure below shows space-time diagrams based on this idea. In a space-time diagram, time is plotted going upward, with the bottom being the distant past. The black lines show the paths of different clumps of matter (galaxies) as function of time. These are called "world-lines". The red lines show the position of light rays that reach us now at the top center of the diagrams. These are called "light cones". Lerner says that only a small region of space collapsed: only a few hundred million light-years across. This is shown on the left. But if this were the case, then the distant galaxy at G would have a recession velocity smaller than the recession velocity of the nearby galaxy A. This is not what we observe. Thus a much larger region must have collapsed. This is shown on the right. Now G has a larger recession velocity than A which matches the observations.

What causes the reversal from collapse to re-expansion? Lerner claims that it is the pressure caused by the annihilation of matter and antimatter during the collapse. The green ellipse shows this high pressure region. But only pressure differences cause forces. A pressure gradient is needed to generate an acceleration. In the case of a large region of collapse, which is needed to match the observations, a larger acceleration requires a larger pressure gradient, and this gradient exists over a larger distance, leading to a greatly increased pressure.
But in relativity pressure has "weight" and causes stronger gravitational attraction. This can be seen using work W = PdV, so the pressure is similar to an energy density. Then through E = mc2, this energy density is similar to a mass density. If the collapsing region is big enough to match the observations, then the pressure must be so large that a black hole forms and the region does not re-expand. Peebles discusses this problem with the plasma cosmology in his book "Principles of Physical Cosmology".
Remarkably, Lerner now disowns the the Alfven-Klein model which plays such a big part in the BBNH, and wants me to give the proper attribution! He points out that he listed problems with the Alfven-Klein model in the Appendix of BBNH, but these were rather minor problems compared to the fact that it just won't work! If the Alfven-Klein model doesn't work, Lerner's fall back is tired light, which is another total failure.
Lerner's model for the CMB claims that the intergalactic medium is a strong absorber of radio waves. His evidence for this is presented in Figure 6.19 of BBNH, which allegedly shows a decrease in the radio to infrared luminosity ratio as function of distance. This absorption is supposed to occur in narrow filaments, with tiny holes scattered about randomly so that distant compact radio sources like QSOs can be seen through the holes.
The best evidence against this model in also in BBNH, in Figure 6.17. This is a picture of Cygnus A, which is the brightest extragalactic radio source. It has a redshift z = 0.056 and is 700 million light years away, using H0 = 75 as in Lerner's ApJ article, and looking at Figure 6.19 of BBNH, we see that it should be more than 99% absorbed. So more than 99% of the area should be blacked out by absorbing filaments in Figure 6.17, but none can be seen. Cygnus A could be plotted on Figure 6.19, but it would be off scale in the upper right corner, completely orthogonal to Lerner's claimed trend.
Lerner has denied the existence of extended high redshift radio sources, which is pretty silly since Cygnus A obviously counts as one. A three times more distant extended radio source is in Abell 2218, with a size of 120" and a redshift of z = 0.174. Clearly this is beyond Lerner's metagalaxy but there is no big hole in the CMB there. The field has been studied extensively for the Sunyaev-Zeldovich effect and the deficit is less than a milliKelvin.
The 3CRR Atlas has images of many distant radio sources with large angular size. The largest angular size for those sources with z > 0.4 is 3C457 which has an angular size of 205" and a redshift of z = 0.428. 7 out of the 10 sources with 0.4 < z < 0.5 in this list have sizes greater than 30". A single 30" hole in the absorbing curtain would have appeared as a -2 mK anisotropy in the Saskatoon data and nothing like this was seen.
Thus radio sources with large angular size are seen to great distances and Lerner's local absorbing curtain does not exist.
A second objection to Lerner's local absorbing curtain is that its density falls inversely with distance from the local density peak, which Lerner takes to be the Virgo supercluster. But if the density of the absorbers peaks at the Virgo, then there will be much more absorption in that direction than in the opposite direction. This would make the distribution of radio sources on the sky very anisotropic. But the radio sources are evenly distributed to within a few percent, so Lerner's local absorbing curtain does not exist.
A third objection to Lerner's local absorbing curtain is that by making distant radio sources fainter, it would change the number vs flux law for radio sources in a way that is not observed. Normally the flux of a source falls off like an inverse square law: F = A/D2, where A is a constant that depends on the luminosity of the source. If you count all the sources brighter than a minimum flux Fmin, then you are looking out to maximum distance Dmax = sqrt(A/Fmin). The number of sources varies like D3, or N = N1(Fmin/F1)-1.5. Lerner changes the flux distance relation to F = A/D2.4 with his added radio absorption, and this would change the number count law to N = N1(Fmin/F1)-1.25. If in addition the density of radio sources peaked near the Earth the way that Lerner assumes other densities do, then the number count law becomes N = N1(Fmin/F1)-0.83. The actual data show N = N1(Fmin/F1)-1.8 which is not compatible with Lerner's model. Thus Lerner's local absorbing curtain does not exist.
Assuming the existence of his absorbing curtain, even though extended distant radio sources show that it does not exist, Lerner (1995, Ap&SS, 227, 61) presents a fit to the FIRAS spectrum of the cosmic microwave background. After discussing how there is a slight variation in "absorbency" (not defined, units unknown) with frequency, Lerner's final fitting function in his Equation (38) assumes an opacity that is independent of frequency. This function has seven apparent parameters in addition to the 2 parameters of temperature and galactic normalization that are needed for any FIRAS fit. Lerner then bins the FIRAS data in Mather et al. (1994) from 34 points down to 10 binned points, and finds that his 9 parameter model gives a good fit to 10 data points. This sounds stupid, but that is mainly due to the paper being poorly written and edited. Lerner's fitting function actually only has two free parameters: a Kompaneets "y" distortion times an emissivity that is slightly different from unity. And the resulting 4 parameter fit to the 34 data points in Mather et al. (1994) is pretty good. The Figure below shows the deviation from a blackbody for Lerner's model, and the open circles are the Mather et al. (1994) data.
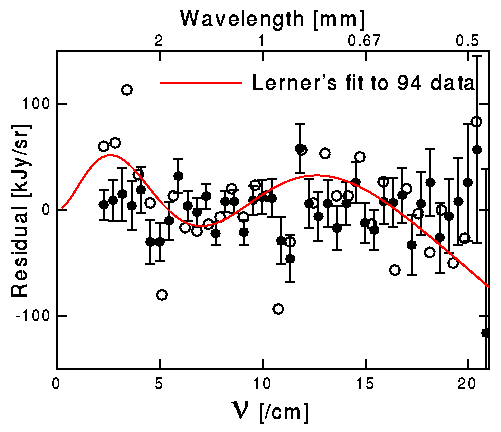
Unfortunately for Lerner, the improved calibration and use of the full FIRAS dataset in Fixsen et al. (1996) give the black data points in the Figure. Lerner's model is a bad fit to this data. The curve shown, which is the best fit to the Mather et al. (1994) data, is six standard deviations away from the Fixsen et al. (1996) data. Readjusting the emissivity and "y" parameter to best fit the Fixsen et al. (1996) data gives a change in chi2 of only 0.7 for two new degrees of freedom, which is worse than the average performance of random models.
Lerner wants to make helium in stars. This presents a problem because the stars that actually release helium back into the interstellar medium make a lot of heavier elements too. Observations of galaxies with different helium abundances show that for every 3.2 grams of helium produced, stars produce 1 gram of heavier elements (French, 1980, ApJ, 240, 41). Thus it is not even possible to make the 28% helium fraction in the Sun without making four times more than the observed 2% heavier elements fraction, and making the 23% helium with only 0.01% of heavier elements seen in old stars in the Milky Way halo is completely out of the question.
But a further problem is that stars make no lithium and no deuterium. Lerner proposes that these elements are made by spallation in cosmic rays. But the cosmic rays have 80 deuterium nuclei for every lithium nucleus (Meyer, 1969, ARAA, 7, 1) while the Universe has about 6 million deuterium nuclei for every lithium nucleus. So if the lithium is entirely due to spallation in cosmic rays, the Universe is still missing 99.99% of the observed deuterium. Lerner's arithmetic once again fails by a large margin.
Top | Criticism | Alternative | Miscellaneous | Bottom
v = (1 - 0.5*(m/E)2+...)*c = 0.999999999999875*cand after traveling for 160,000 years lags by less than 1 second. The observed burst was 6-10 seconds long, so even the electron neutrino could have enough mass to be the hot component in a mixed dark matter model.
Top | Criticism | Alternative | Miscellaneous | Bottom
Tutorial:
Part 1 |
Part 2 |
Part 3 |
Part 4
FAQ |
Age |
Distances |
Bibliography |
Relativity
© 1997-2000 Edward L. Wright. Last modified 11 Oct 2003