Part 1: Observations of Global Properties
Part 2: Homogeneity and Isotropy; Many Distances; Scale Factor
Part 3: Spatial Curvature; Flatness-Oldness; Horizon
Part 4: Inflation; Anisotropy and Inhomogeneity
FAQ | Tutorial : Part 1 | Part 2 | Part 3 | Part 4 | Age | Distances | Bibliography | Relativity
The Cosmological Principle:
To say the Universe is homogeneous means that any measurable property of the Universe is the same everywhere. This is only approximately true, but it appears to be an excellent approximation when one averages over large regions. Since the age of the Universe is one of the measurable quantities, the homogeneity of the Universe must be defined on a surface of constant proper time since the Big Bang. Time dilation causes the proper time measured by an observer to depend on the velocity of the observer, so we specify that the time variable t in the Hubble law is the proper time since the Big Bang for comoving observers.
With the correct interpretation of the variables, the Hubble law (v = HD) is true for all values of D, even very large ones which give v > c. But one must be careful in interpreting the distance and velocity. The distance in the Hubble law must be defined so that if A and B are two distant galaxies seen by us in the same direction, and A and B are not too far from each other, then the difference in distances from us, D(A)-D(B), is the distance A would measure to B. But this measurement must be made "now" -- so A must measure the distance to B at the same proper time since the Big Bang as we see now. Thus to determine Dnow for a distant galaxy Z we would find a chain of galaxies ABC...XYZ along the path to Z, with each element of the chain close to its neighbors, and then have each galaxy in the chain measure the distance to the next galaxy at time to since the Big Bang. The distance to Z, D(us to Z), is the sum of all these subintervals:
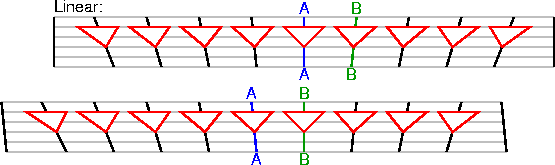
Dnow = D(us to Z) = D(us to A) + D(A to B) + ... D(X to Y) + D(Y to Z)And the velocity in the Hubble law is just the change of Dnow per unit time. It is close to cz for small redshifts but deviates for large ones. The space-time diagram below repeats the example from Part 1 showing how a change in point-of-view from observer A to observer B leaves the linear velocity vs. distance Hubble law unchanged:

The time and distance used in the Hubble law are not the same as the
x and t used in special relativity, and this often leads to confusion.
In particular, galaxies that are far enough away from us necessarily
have velocities greater than the speed of light:
v = HoDnow Dnow = (c/Ho)ln(1+z) 1+z = exp(v/c)Note that the redshift-velocity law is not the special relativistic Doppler shift law
1+z = sqrt[(1+v/c)/(1-v/c)]which only applies to special relativistic coordinates, not to cosmological coordinates.
While the Hubble law distance is in principle measurable, the need for helpers all along the chain of galaxies out to a distant galaxy makes its use quite impractical. Other distances can be defined and measured more easily. One is the angular size distance, defined by
theta = size/DA so DA = size/thetawhere "size" is the transverse extent of an object and "theta" is the angle (in radians) that it subtends on the sky. For the zero density model, the special relativistic x is equal to the angular size distance, x = DA.
Another important distance indicator is the flux received from an object, and this defines the luminosity distance DL through
Flux = Luminosity/(4*pi*DL2)A fourth distance is based on the light travel time: Dltt = c*(to-tem). People who say that the greatest distance we can see is c*to are using this distance. But Dltt = c*(to-tem) is not a very useful distance because it is very hard to determine tem, the age of the Universe at the time of emission of the light we see. And finally, the redshift is a very important distance indicator, since astronomers can measure it easily, while the size or luminosity needed to compute DA or DL are always very hard to determine. The redshift is such a useful distance indicator that it is a shame that science journalists conspire to leave it out of stories: they must be taught the "5 w's but no z" rule in journalism school.
The predicted curve relating one distance indicator to another depends on the cosmological model. The plot of redshift vs distance for Type Ia supernovae shown earlier is really a plot of cz vs DL, since fluxes were used to determine the distances of the supernovae. This data clearly rule out models that do not give a linear cz vs DL relation for small cz. Extension of these observations to more distant supernovae have started to allow us to measure the curvature of the cz vs DL relation, and provide more valuable information about the Universe.
The perfect fit of the CMB to a blackbody allows us to determine the DA vs DL relation. Since the CMB is produced at great distance but still looks like a blackbody, a distant blackbody must look like a blackbody (even though the temperature will change due to the redshift). The luminosity of blackbody is
L = 4*pi*R2*sigma*Tem4where R is the radius, Tem is the temperature of the emitting blackbody, and sigma is the Stephan-Boltzmann constant. If seen at a redshift z, the observed temperature will be
Tobs = Tem/(1+z)and the flux will be
F = theta2*sigma*Tobs4where the angular radius is related to the physical radius by
theta = R/DACombining these equations gives
DL2 = L/(4*pi*F)
= (4*pi*R2*sigma*Tem4)/(4*pi*theta2*sigma*Tobs4)
= DA2*(1+z)4
or
DL = DA*(1+z)2
Models that do not predict this relationship between DA
and DL, such
as the chronometric model or the
tired light model, are ruled out by the
properties of the CMB.
Here is a
Javascript calculator that takes
Ho,
OmegaM,
the normalized
cosmological constant lambda
and the redshift z
and then computes all of the these distances.
Here are the technical formulae
for these distances.
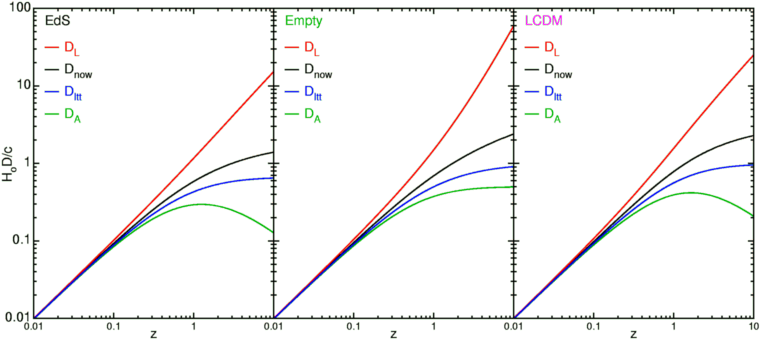
The graphs below show these
distances vs. redshift for three models: the critical density matter
dominated Einstein - de Sitter model (EdS), the empty model, and the
accelerating
Lambda-CDM
model (LCDM) that is the current consensus model.
Because the velocity or dDnow/dt is strictly proportional to Dnow, the distance between any pair of comoving objects grows by a factor (1+H*dt) during a time interval dt. This means we can write the distance to any comoving observer as
DG(t) = a(t)*DG(to)where DG(to) is the distance Dnow to galaxy G now, while a(t) is universal scale factor that applies to all comoving objects. From its definition we see that a(to) = 1.
We can compute the dynamics of the Universe by considering an object with distance D(t) = a(t) Do. This distance and the corresponding velocity dD/dt are measured with respect to us at the center of the coordinate system. The gravitational acceleration due to the spherical ball of matter with radius D(t) is g = -G*M/D(t)2 where the mass is M = 4*pi*D(t)3*rho(t)/3. Rho(t) is the density of matter which depends only on the time since the Universe is homogeneous. The mass contained within D(t) is independent of the time since the interior matter has slower expansion velocity while the exterior matter has higher expansion velocity and thus stays outside. The gravitational effect of the external matter vanishes: the gravitational acceleration inside a spherical shell is zero, and all the matter in the Universe with distance from us greater than D(t) can be represented as union of spherical shells. With a constant mass interior to D(t) producing the acceleration of the edge, the problem reduces to the problem of a body moving radially in the gravitational field of a point mass. If the velocity is less than the escape velocity, the expansion will stop and recollapse. If the velocity equals the escape velocity we have the critical case. This gives
v = H*D = v(esc) = sqrt(2*G*M/D)
H2*D2 = 2*G*(4*pi/3)*rho*D2 or
rho(crit) = 3*H2/(8*pi*G)
For rho less than or equal to the
critical density rho(crit),
the Universe expands forever,
while for rho greater than rho(crit), the Universe will eventually
stop expanding and recollapse. The value of rho(crit) for
Ho = 71 km/sec/Mpc is 9E-30 = 9*10-30 gm/cc
or 6 protons per cubic meter
or 1.4E11 = 1.4*1011 solar masses per cubic
Megaparsec. The latter can be compared to the observed
1.85E8 = 1.85*108
solar luminosities per Mpc3, requiring a mass-to-light ratio
of 760 in solar units to close the Universe.
If the density is anywhere close to critical most of the matter
must be too dark to be observed.
Current density estimates suggest that
the matter density is between 0.2 to 1 times the critical density, and this
does require that most of the matter in the Universe is dark.
FAQ | Tutorial : Part 1 | Part 2 | Part 3 | Part 4 | Age | Distances | Bibliography | Relativity
© 1996-2009 Edward L. Wright. Last modified 12 Jun 2009