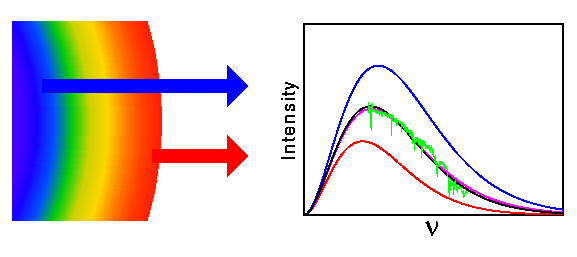
The CMB radiation is such a perfect fit to a blackbody that it cannot be
made by stars. The reason for this is that stars are at best only
pretty good blackbodies, and the usual absorption lines and band edges
make them pretty bad blackbodies. In order for a star to radiate it
must have a temperature gradient in its outer regions, as shown below:

One can easily have stars visible from different redshifts which will smooth out the absorption lines, but these stars will appear as different temperature blackbodies and it is the mixing of different apparent temperatures that causes the deviation of the purple curve. Hence more mixing will make things worse.
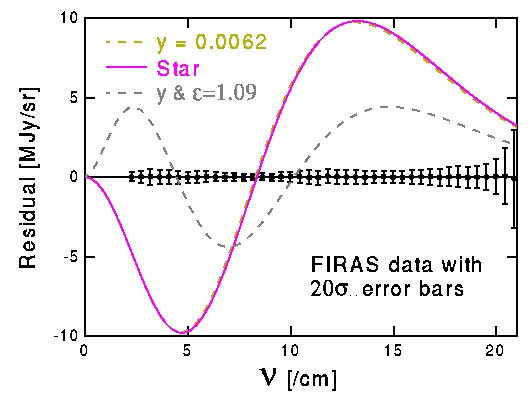
The gray dashed curve on the plot shows how much the fit can be improved by adjusting the emissivity or sky coverage of the stars. Normally the emissivity is 1-R where R is the reflectance, and thus the emissivity usually has to be less than 1. But the best fit emissivity is 1.09. So this would be unphysical unless the redshift is caused by tired light. In this case the apparent emissivity is (1+z)3 >> 1, and one can lower this down to an apparent emissivity of 1.09 by only partly covering the sky with stars. This requires some fine tuning, since for a typical stellar temperature of 4000 K a redshift of 1+z = 1466 is needed which gives an apparent emissivity of 3,150,662,696 that needs to be canceled by a sky coverage of 0.00000000034511 in this model. But the errors in the CMB fit are still 300 times larger than the FIRAS data allow, so this model can also be ruled out.
How does the Big Bang produce a nearly perfect blackbody CMB? In the Big Bang model there are no temperature gradients because the Universe is homogeneous. While the temperature varies with time, this variation is exactly canceled by the redshift so the apparent temperature of radiation from redshift z is given by T(z)/(1+z) which is equal to the CMB temperature To for all redshifts which contribute to the CMB.
FAQ | Tutorial : Part 1 | Part 2 | Part 3 | Part 4 | Age | Distances | Bibliography | Relativity