Cosmic Microwave Background
The cosmic microwave background (CMB) is a key prediction
of the hot Big Bang model, and the most important
observation that discriminates between the Big Bang and
the Steady State
models. So it is an interesting historical
anomaly that this prediction was not put forward and tested
by the inventors of either theory, and that the first
observers of the CMB were completely unaware of its cosmological
significance.
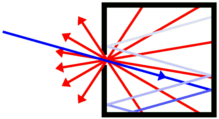 The CMB has the spectrum of a
blackbody. A blackbody spectrum is produced by an isothermal,
opaque and non-reflecting object. Usually a cavity with a small hole
is used in the laboratory to make an opaque and non-reflective object.
Radiation that enters the cavity through the hole will have to bounce
off many walls before it returns to the outside, so even if the walls
are only somewhat dark, the hole will appear to be completely black.
The diagram at right shows such a cavity, with the blue incoming ray
being absorbed completely while the red rays show the outgoing thermal
radiation. A simple gedanken experiment shows that the
spectrum emitted by a blackbody can only depend on its temperature T.
The proof first assumes that two blackbodies have different spectra and
then shows that this leads to a contradiction. Let two blackbodies A
& B, both at temperature T, radiate different spectra. Then use a
filter and aperture stops to allow them to transfer heat only by
radiation in a given passband. Then the radiation of A is entirely
absorbed by B, and the radiation of B is entirely absorbed by A. Thus
if their spectra are different, there would be a net transfer of heat
between A & B, but their temperatures are the same. Since heat
transfer between objects of the same temperature does not occur, the
spectra must be identical. The choice of filter passband was
arbitrary, so the spectra must be identical at all frequencies. This
universal blackbody spectrum was clearly a very important topic in
physics at the end of the 19th century, and Planck was studying
blackbody radiation when he introduced the idea of quanta, and
defined the quantum of action h which we now know as Planck's
constant. Because of the universality of the blackbody spectrum, we
can convert any spectral measurement into a brightness
temperature at the measured wavelength. The unique character of a
blackbody spectrum is that the brightness temperature of a blackbody is the
same at all wavelengths.
When talking about the CMB scientists always use the Kelvin scale of
temperature, which is just like the Celsius scale except the zero point
is absolute zero instead of the freezing point of water at
Tice = 273.15 K.
The CMB has the spectrum of a
blackbody. A blackbody spectrum is produced by an isothermal,
opaque and non-reflecting object. Usually a cavity with a small hole
is used in the laboratory to make an opaque and non-reflective object.
Radiation that enters the cavity through the hole will have to bounce
off many walls before it returns to the outside, so even if the walls
are only somewhat dark, the hole will appear to be completely black.
The diagram at right shows such a cavity, with the blue incoming ray
being absorbed completely while the red rays show the outgoing thermal
radiation. A simple gedanken experiment shows that the
spectrum emitted by a blackbody can only depend on its temperature T.
The proof first assumes that two blackbodies have different spectra and
then shows that this leads to a contradiction. Let two blackbodies A
& B, both at temperature T, radiate different spectra. Then use a
filter and aperture stops to allow them to transfer heat only by
radiation in a given passband. Then the radiation of A is entirely
absorbed by B, and the radiation of B is entirely absorbed by A. Thus
if their spectra are different, there would be a net transfer of heat
between A & B, but their temperatures are the same. Since heat
transfer between objects of the same temperature does not occur, the
spectra must be identical. The choice of filter passband was
arbitrary, so the spectra must be identical at all frequencies. This
universal blackbody spectrum was clearly a very important topic in
physics at the end of the 19th century, and Planck was studying
blackbody radiation when he introduced the idea of quanta, and
defined the quantum of action h which we now know as Planck's
constant. Because of the universality of the blackbody spectrum, we
can convert any spectral measurement into a brightness
temperature at the measured wavelength. The unique character of a
blackbody spectrum is that the brightness temperature of a blackbody is the
same at all wavelengths.
When talking about the CMB scientists always use the Kelvin scale of
temperature, which is just like the Celsius scale except the zero point
is absolute zero instead of the freezing point of water at
Tice = 273.15 K.
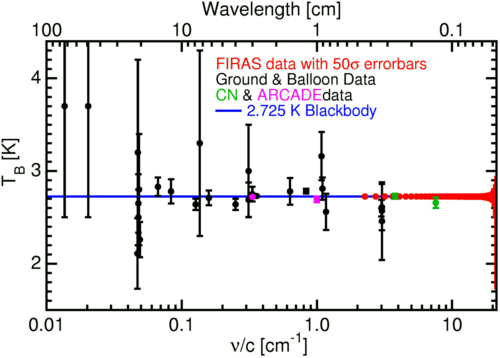
The graph above shows the measured brightness temperature
TB of the CMB at many different wavelengths.
Clearly TB = 2.725 K is consistent with all the data
within the statistical scatter expected for the stated errors.
In order to make a blackbody spectrum, an object as to be opaque,
non-reflective and isothermal. Thus a star, which is opaque,
does not
produce a blackbody spectrum because we can see both cooler outer
layers and hotter deeper layers. But even though the
temperature of
the Universe changes as it evolves, with TCMB =
To (1+z), the Universe looks isothermal because the
redshifting of radiation makes the warmer but redshifted distant
Universe appear to have exactly the same temperature as the Universe
today.
The
FIRAS instrument on
COBE had a large conical horn for collecting
the cosmic microwave background. There was only a small hole in the
end of the horn to let the radiation into the instrument. But FIRAS
also carried a microwave absorber, the external calibrator or XCAL,
that could be inserted into the horn like a trumpet mute, and heaters
that could make the whole horn+plus absorber cavity isothermal. When
the XCAL was in the horn FIRAS observed a very good blackbody cavity,
but when the XCAL was out FIRAS observed the CMB. No signifcant
difference could be seen. The CMB is very close to a blackbody with
temperature 2.725 K.
The FIRAS results are shown below in units of intensity (power per
unit area per unit frequency per unit solid angle) vs.
frequency and/or wavelength.
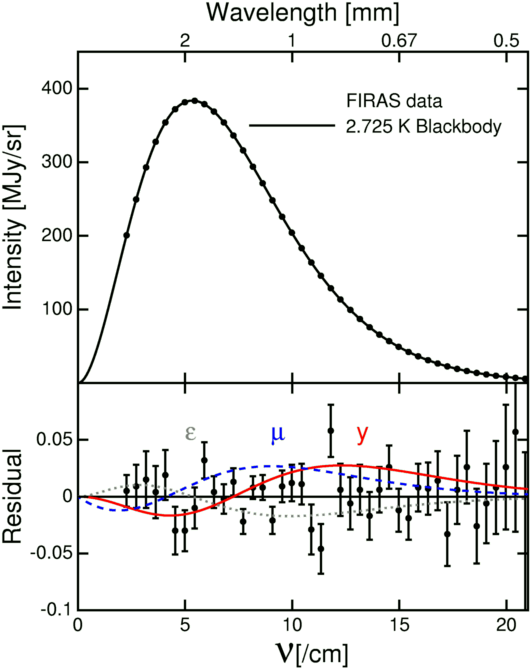
Eric Adelberger
would like me to point out that the fundamental FIRAS
measurement is the residual plot at the bottom. This is what FIRAS
actually measured: the difference between the CMB and the best fitting
blackbody.
The plot at top shows this residual added to the theoretical blackbody
spectrum at the best fitting XCAL temperature, based on the function
derived by Planck in 1900. The three curves in the bottom correspond
to three fairly likely non-blackbody spectra: the grey curve shows a
body with a reflectivity of 100 parts per million instead of zero, and
the red and blue curves show the effect of hot electrons
adding an excess 60 parts per million of energy to the CMB either before
(blue) or after (red) 1000 years after the Big Bang. These curves show
the maximum distortions allowed by the FIRAS data.
History
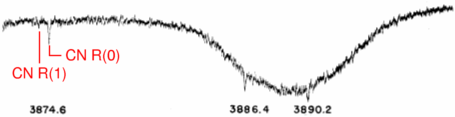 The first observations of the CMB were made by McKellar using
interstellar molecules in 1940. The image at right shows a
spectrum of the star zeta Oph taken in 1940 which shows the weak R(1)
line from rotationally excited CN. The significance of these
data was not realized at the time, and there is even a line in the
1950 book Spectra of Diatomic Molecules by the Nobel-prize winning
physicist Gerhard Herzberg, noting the 2.3 K rotational
temperature of the cyanogen molecule (CN) in interstellar space
but stating that it had "only a very restricted meaning."
We now know that this molecule is primarily excited by the
CMB implying a brightness temperature of
To = 2.729 +/- 0.027 K at a
wavelength of 2.64 mm (
Roth, Meyer & Hawkins 1993).
The first observations of the CMB were made by McKellar using
interstellar molecules in 1940. The image at right shows a
spectrum of the star zeta Oph taken in 1940 which shows the weak R(1)
line from rotationally excited CN. The significance of these
data was not realized at the time, and there is even a line in the
1950 book Spectra of Diatomic Molecules by the Nobel-prize winning
physicist Gerhard Herzberg, noting the 2.3 K rotational
temperature of the cyanogen molecule (CN) in interstellar space
but stating that it had "only a very restricted meaning."
We now know that this molecule is primarily excited by the
CMB implying a brightness temperature of
To = 2.729 +/- 0.027 K at a
wavelength of 2.64 mm (
Roth, Meyer & Hawkins 1993).
Later Robert Dicke made measurements that could have discovered the
CMB. He measured the brightness temperature of the sky as a function
of the elevation angle. As his antenna pointed closer to the horizon
the brightness temperature went up and became closer to the air
temperature. Dicke used a low sidelobe flared horn, and he invented a
rapidly switching differential radiometer for this work, now known as a
Dicke radiometer, that switched between the sky and an ambient
temperature (300 K) load. Using this data Dicke determined the
absorption of the atmosphere at 1 to 1.5 cm wavelength and showed that
this microwave "K band" could be used for radar. The short wavelength
allowed radars to fit inside fighter planes and greatly aided the Allied
war effort in WW II. Dicke was not interested in the temperature of
the sky outside the atmosphere but in 1946
Dicke et al. published an upper limit
on the brightness temperature of the sky:
Tsky < 20 K.
By using a room temperature load Dicke had a large difference
signal at the zenith, and a few percent uncertainty in his absolute
gain calibration generated a several Kelvin uncertainty in the sky
temperature.
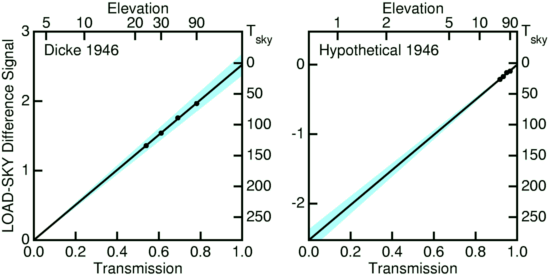
The plot on the left above is the actual data from Figure 3 of the
Dicke et al. (1946), although I had to do a fit to find
the baseline that was subtracted. As you can see, the extrapolation
to 100% transmission is large because of the water vapor absorption
and the chopped signal at 100% transmission is large so the gain
uncertainty shown in blue leads to a large uncertainty in Tsky.
On the right is a hypothetical experiment that could have been done
in 1945 with a cold reference at a wavelength not on the water
vapor line.
If Dicke had used a low temperature load and had observed
from a mountaintop instead of Florida, he would have detected the CMB.
Ironically, the
paper by Gamow describing the hot Big Bang occurs in the same
volume of the Physical Review. A later paper by
Alpher, Bethe & Gamow describing the hot Big Bang is one of the
classic jokes in physics: Gamow added Bethe's name to this paper just
to make it sound like alpha, beta, gamma. Bethe actually didn't do any
work on it.
A further irony is that one person did make the connection between
McKellar's 2.3 K and the Universe, and that was
Fred Hoyle in a 1950
review (1950, Observatory, 70, 194-195)
of a book by
Gamow and Critchfield (1949, "Theory of Atomic
Nucleus and Nuclear Energy-Sources"). Hoyle was one of the three inventors
of the Steady State model which was the
main competitor to Gamow's Big Bang model. Hoyle wrote: "[the Big Bang model]
would lead to a temperature of the radiation at present
maintained throughout the whole of space much greater than McKellar's
determination for some regions within the Galaxy."
The appendix with Gamow's
cosmological model gives values from which To = 11
K can be computed, which certainly
is larger than the observation of 2.3 K.
But Hoyle did not consider Alpher and Herman's
paper (1949, Phys. Rev., 75, 1089-1095) which gave two versions of the
Big Bang, one with To = 1 K
and one with To = 5 K.
Thus the uncertainties in the cosmological parameters easily
allowed for McKellar's CN data to be a confirmation of the Big Bang
instead of a refutation of it. But none of the participants in this
debate ever looked further into the interstellar CN data, and thus the
CMB remained undiscovered until 1965. In fact Gamow seemed to
conspicuously ignore this discrepancy, and gives To =
50 K in his book "Creation of the Universe" (1955, 1961).
Penzias & Wilson were studying the radiation collected by a large
horn antenna in New Jersey when they found an excess radiation at 7.35 cm
wavelength that was
equivalent to a 3.5 +/- 1 K blackbody. Their horn had low
sidelobes, and Penzias & Wilson switched against a low temperature
reference load. They did not know what this excess meant, but spoke to
Bernie Burke of MIT, who knew that Dicke was now leading a group
planning to measure the CMB. Ironically Dicke had forgotten about his
old upper limit, but he knew how to do the measurement. But before his
group could finish building their instrument, Dicke got a call from
Penzias & Wilson. After hearing about their data, Dicke said:
"Boys, we've been scooped." Papers by
Penzias & Wilson and by
Dicke, Peebles, Roll & Wilkinson describing these results appeared
in the 1965 Astrophysical Journal. Wilkinson went on to
measure the CMB at a large number of wavelengths and always found the
same brightness temperature over a wide range of wavelengths.
Claims that Le Roux measured the CMB in the 1950's are incorrect.
Le Roux used an ordinary parabolic dish, which is not designed
for very low sidelobes, and used the horizon as an absolute
temperature reference. He also observed at 900 MHz where the galactic
foreground is very bright. While Le Roux's unpublished thesis gives
Tsky = 3 +/- 1 K, the first published
version (Denisse, Lequeux & Le Roux, 1957, Comptes Rendus, 244, 3033)
gives Tsky < 3 K. Both of these results are
incorrect because the galactic foreground makes the minimum temperature
of the sky > 4 K at this frequency. A more complete
published version gives Tsky < 20 K
("une vingtaine").
This is a more reasonable assessment of the precision of these data.
Tutorial:
Part 1 |
Part 2 |
Part 3 |
Part 4
FAQ |
Age |
Distances |
Bibliography |
Relativity
Ned Wright's home page
© 2007-2009
Edward L. Wright.
Last modified on 24 Oct 2009
 The CMB has the spectrum of a
blackbody. A blackbody spectrum is produced by an isothermal,
opaque and non-reflecting object. Usually a cavity with a small hole
is used in the laboratory to make an opaque and non-reflective object.
Radiation that enters the cavity through the hole will have to bounce
off many walls before it returns to the outside, so even if the walls
are only somewhat dark, the hole will appear to be completely black.
The diagram at right shows such a cavity, with the blue incoming ray
being absorbed completely while the red rays show the outgoing thermal
radiation. A simple gedanken experiment shows that the
spectrum emitted by a blackbody can only depend on its temperature T.
The proof first assumes that two blackbodies have different spectra and
then shows that this leads to a contradiction. Let two blackbodies A
& B, both at temperature T, radiate different spectra. Then use a
filter and aperture stops to allow them to transfer heat only by
radiation in a given passband. Then the radiation of A is entirely
absorbed by B, and the radiation of B is entirely absorbed by A. Thus
if their spectra are different, there would be a net transfer of heat
between A & B, but their temperatures are the same. Since heat
transfer between objects of the same temperature does not occur, the
spectra must be identical. The choice of filter passband was
arbitrary, so the spectra must be identical at all frequencies. This
universal blackbody spectrum was clearly a very important topic in
physics at the end of the 19th century, and Planck was studying
blackbody radiation when he introduced the idea of quanta, and
defined the quantum of action h which we now know as Planck's
constant. Because of the universality of the blackbody spectrum, we
can convert any spectral measurement into a brightness
temperature at the measured wavelength. The unique character of a
blackbody spectrum is that the brightness temperature of a blackbody is the
same at all wavelengths.
When talking about the CMB scientists always use the Kelvin scale of
temperature, which is just like the Celsius scale except the zero point
is absolute zero instead of the freezing point of water at
Tice = 273.15 K.
The CMB has the spectrum of a
blackbody. A blackbody spectrum is produced by an isothermal,
opaque and non-reflecting object. Usually a cavity with a small hole
is used in the laboratory to make an opaque and non-reflective object.
Radiation that enters the cavity through the hole will have to bounce
off many walls before it returns to the outside, so even if the walls
are only somewhat dark, the hole will appear to be completely black.
The diagram at right shows such a cavity, with the blue incoming ray
being absorbed completely while the red rays show the outgoing thermal
radiation. A simple gedanken experiment shows that the
spectrum emitted by a blackbody can only depend on its temperature T.
The proof first assumes that two blackbodies have different spectra and
then shows that this leads to a contradiction. Let two blackbodies A
& B, both at temperature T, radiate different spectra. Then use a
filter and aperture stops to allow them to transfer heat only by
radiation in a given passband. Then the radiation of A is entirely
absorbed by B, and the radiation of B is entirely absorbed by A. Thus
if their spectra are different, there would be a net transfer of heat
between A & B, but their temperatures are the same. Since heat
transfer between objects of the same temperature does not occur, the
spectra must be identical. The choice of filter passband was
arbitrary, so the spectra must be identical at all frequencies. This
universal blackbody spectrum was clearly a very important topic in
physics at the end of the 19th century, and Planck was studying
blackbody radiation when he introduced the idea of quanta, and
defined the quantum of action h which we now know as Planck's
constant. Because of the universality of the blackbody spectrum, we
can convert any spectral measurement into a brightness
temperature at the measured wavelength. The unique character of a
blackbody spectrum is that the brightness temperature of a blackbody is the
same at all wavelengths.
When talking about the CMB scientists always use the Kelvin scale of
temperature, which is just like the Celsius scale except the zero point
is absolute zero instead of the freezing point of water at
Tice = 273.15 K.


 The first observations of the CMB were made by McKellar using
interstellar molecules in 1940. The image at right shows a
spectrum of the star zeta Oph taken in 1940 which shows the weak R(1)
line from rotationally excited CN. The significance of these
data was not realized at the time, and there is even a line in the
1950 book Spectra of Diatomic Molecules by the Nobel-prize winning
physicist Gerhard Herzberg, noting the 2.3 K rotational
temperature of the cyanogen molecule (CN) in interstellar space
but stating that it had "only a very restricted meaning."
We now know that this molecule is primarily excited by the
CMB implying a brightness temperature of
To = 2.729 +/- 0.027 K at a
wavelength of 2.64 mm (
The first observations of the CMB were made by McKellar using
interstellar molecules in 1940. The image at right shows a
spectrum of the star zeta Oph taken in 1940 which shows the weak R(1)
line from rotationally excited CN. The significance of these
data was not realized at the time, and there is even a line in the
1950 book Spectra of Diatomic Molecules by the Nobel-prize winning
physicist Gerhard Herzberg, noting the 2.3 K rotational
temperature of the cyanogen molecule (CN) in interstellar space
but stating that it had "only a very restricted meaning."
We now know that this molecule is primarily excited by the
CMB implying a brightness temperature of
To = 2.729 +/- 0.027 K at a
wavelength of 2.64 mm (