Bayes's Theorem
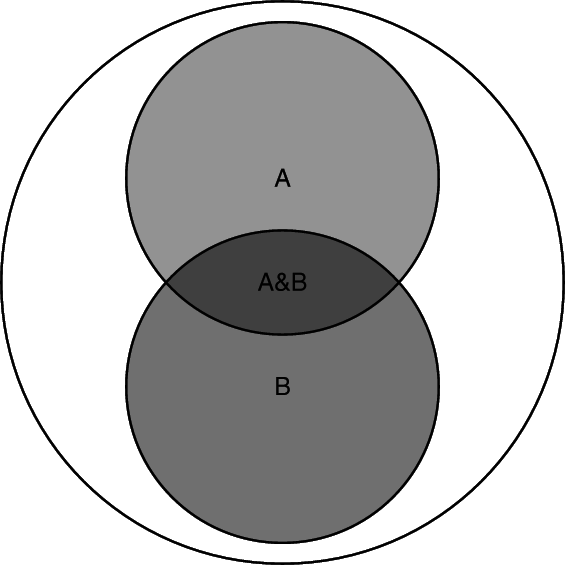
Prob of A&B = (Prob of A) times (Prob of B given A)
P(A&B) = P(A)P(B|A) = P(B)P(A|B)



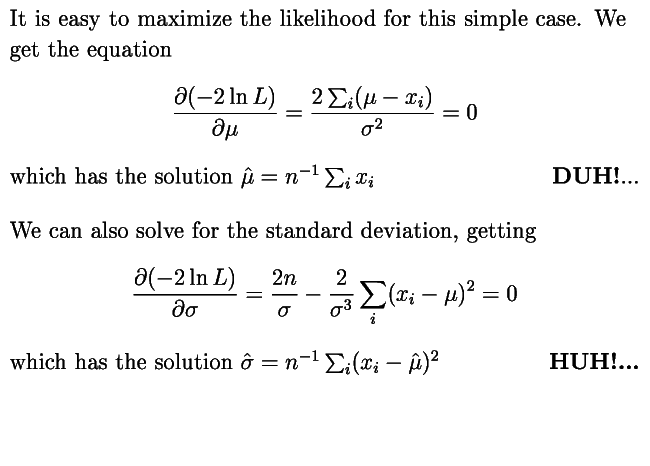
There are 4 kinds of lies:
Q: What is a statistic?
A: A function of one or more random variables.
Usually statistics are designed to extract useful information from a noisy collection of data, such as using the median to find the central value of a set of measurements.

Q: Who was Bayes?
A: Thomas Bayes, 1702-1761, a Presbyterian minister.
Bayes was elected
a Fellow of the Royal Society in 1742 despite the fact that at that time
he had no published works on mathematics, indeed none were published in
his lifetime under his own name.
Bayes set out his theory of probability in Essay towards solving a
problem in the doctrine of chances published in the Philosophical
Transactions of the Royal Society of London in 1764. The paper was sent
to the Royal Society by Richard Price, a friend of Bayes', who wrote:
I now send you an essay which I have found among the papers of our
deceased friend Mr Bayes, and which, in my opinion, has great merit...




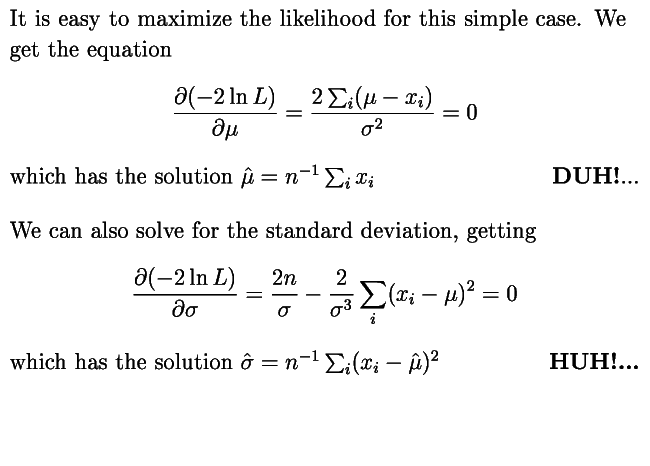
Thus the MLE (maximum likelihood estimator) for the centroid is the mean when the data are Gaussian, but the MLE for the standard deviation is biased -- the prefactor should be (n-1)-1. But for large data sets this error goes away, so the MLE's are said to be asymptotically unbiased. But if you divide your data into a large number of subsets, and get MLE's for each subset, and then average the estimators, this bias can get to be statistically significant.
MLE's are also efficient, so they are generally good things to use.



This situation occurs in practice when data are digitized with a least significant bit that is larger than the actual noise. If you have data taken under these circumstances, you should consider using minimax fitting, where you minimize the maximum absolute value of the error instead of minimizing the sum of the squares of the errors.




If one does two independent experiments, then the combined likelihood of
the two experiments is
L(M) = L1(M) L2(M)
because they are independent.
So if experiment 1 was done prior to our experiment, we could use
L1(M) as the prior distribution in Bayesian statistics.
However, it is a good idea to have separate discussions of what our experiment says about the models, and what the combination of all experiments say about the models. Our experiment is well described by the likelihood function for our data. The combination of all experiments is well described by the product of all their likelihood functions.
If these experiments are any good, then the combined likelihood will be sharply peaked. But if the experiments are not very definitive, then a priori assumptions about the model can determine the most likely case. These assumptions can be codified in the prior distribution. Since the Bayesian approach gives us a place to put our a priori assumptions, it encourages us to think about them, which is generally a good thing. but if the choice of the prior distribution has a significant effect on the outcome, then we just don't have enough data.


Since I like to think that observations do matter, I take this with a BIG grain of salt.





Cosmology FAQ | Tutorial : Part 1 | Part 2 | Part 3 | Part 4 | Age | Distances | Bibliography | Relativity