Power Law a(t)

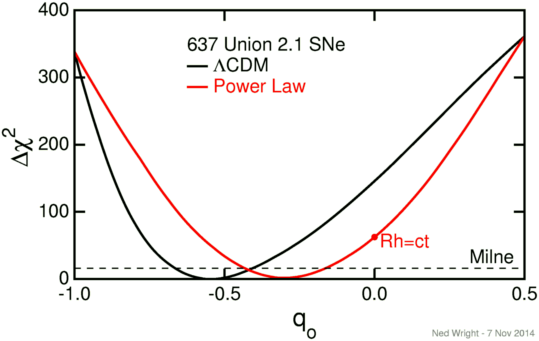
Many authors get taken up with the idea that a power law for the scale factor versus time

a(t) = (t/t_o)ⁿ

gives a good fit to the supernova data in a flat Universe. If n > 1 this is an accelerating Universe and thus can give a not bad fit. The luminosity distance vs. redshift for this model is

D_L(z) = (c/H_o)(1+z)[(1+z)^1-1/n-1]/(1-1/n)

and it gives the goodness of fits shown in the graph below:

This plot shows the Δχ² vs. q_o for both ΛCDM and power law models. The Rh=ct model of Melia specifies n=1, and it is not a good fit to the SNe data as shown by the red dot. For ΛCDM

q_o = Ω_m/2-Ω_v = 1.5*Ω_m - 1

while for power law models

q_o = (1-n)/n

Note that the Einstein-de Sitter model is in both families (n = 2/3, Ω_m = 1, q_o = 0.5) as is the de Sitter model (n = infinity, Ω_m = 0, q_o = -1).

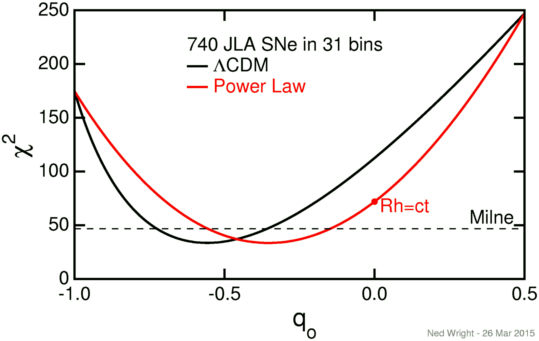
A later supernova dataset (JLA with 740 SNe) gives much the same picture as shown in the figure below:

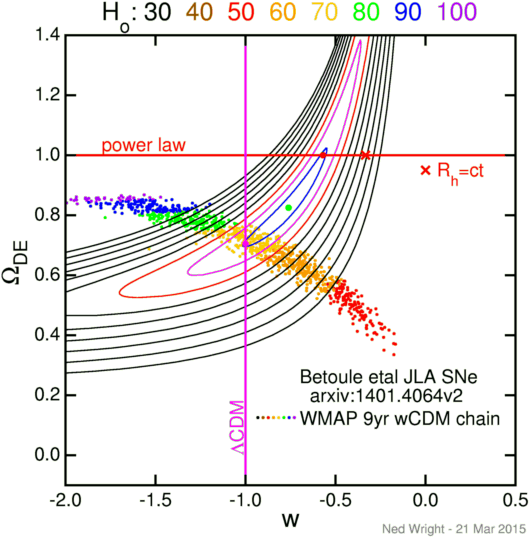
Again the red dot shows a non-accelerating power law model with n = 1, which fails to fit the SNe data and should be rejected. Accelerating power law models with n close to 1.4 do fit the latest supernova dataset.

A problem with the accelerating power law models is that they completely destroy the agreement between the CMB angular power spectrum and the observations. The time of last scattering is much too late, so the acoustic scale is too long. For example, if n = 5/4, then z = 1089 occurs at 50 Myr instead of 0.4 Myr so the acoustic scale is off by a factor of 125. This is illustrated below with a plot of the dark energy fraction Ω_DE vs. the equation of state w for flat wCDM models.

When Ω_DE = 1, then different values of w give different power law a(t) models, with w = -1/3 giving the Rh=ct model with n=1, while w=0 gives the Einstein-de Sitter model with n=2/3. Models with w=-1 gives the flat ΛCMD models. The contours are from fitting the recent JLA sample of SNe, and both the best-fit power law and the best-fit LCDM model are at the 1σ contour with χ² = χ²_min+1, while Rh=ct is close to the 7σ contour. But the rainbow spray of dots is a subsample from the wCDM Monte Carlo Markov Chain based on fitting the WMAP 9 year data, and this clearly stays far away from the power law models at Ω_DE = 1.

Finally, the current model independent estimates for the age of the Universe and the Hubble constant actually give H_o t_o close to 1 while the power law model wants H_o t_o = n which is too high for models that come close to fitting the supernova data. The weighted mean age is t_o = 12.94 +/- 0.75 Gyr while the Hubble constant is 72 +/- 4 km/sec/Mpc using a weighted mean of 73 +/- 4(stat) +/- 5(sys) from Riess et al. (2005) and 71 +/- 5 from Wright (2007). These values give H_o t_o = 0.95 +/- 0.08 which excludes the n = 1.25 model by more than 3σ.