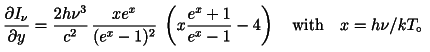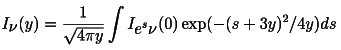Sunyaev-Zeldovich Spectrum
The Sunyaev-Zeldovich effect involves scattering of CMB
photons by rapidly moving electrons in the hot gas
in clusters of galaxies.
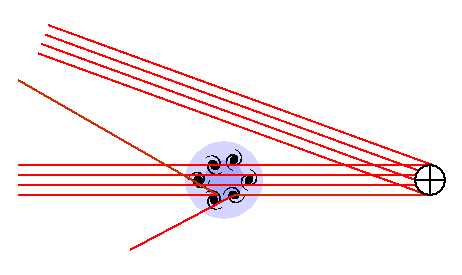
The diagram above shows a cartoon version of this effect.
It is possible to use a combination of the Sunyaev-Zeldovich effect
and the X-ray emission from the hot gas to derive a
distance to the cluster.
This effect is
proportional to (1) the number density of electrons, (2) the thickness
of the cluster along our line of sight, and (3) the electron
temperature. The parameter that combines these factors is called the
Kompaneets y parameter,
with y = τ*(kT/mc2). Tau (τ) is the
optical depth or the fraction of photons scattered, while (kT/mc2)
is the electron temperature in units of the rest mass of the electron.
The usual order of magnitude for y is about 0.0001, which is
very small.
Many years ago
Sunyaev and Zeldovich (1980, ARAA, 18, 537)
published a figure similar to the one below.
This figure still appears in print, for example as Figure 1 in
Carlstrom, Holder and Reese (2002, ARAA, 40, 643).
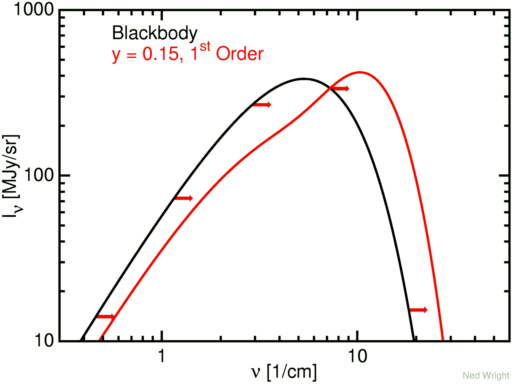
I am not clear about the purpose of the arrows in the figure but I
have put them in to make my version of the figure more like the
Sunyaev and Zeldovich figure. This figure is drawn with a very large
value of y = 0.15.
Unfortunately the distorted spectrum in red was computed using the
first order approximation
[Eqn (A7) in S-Z (1980)] to the Sunyaev-Zeldovich effect, and this
is a poor approximation for y = 0.15, as shown in the figure
below which plots both the first order approximation and the exact
spectrum in blue, computed using Eqn (A8) of S-Z (1980).
The actual shape of the distorted spectrum is always
a widened, lowered and shifted to the right version of the input
spectrum. Note that the mean photon energy is increased by
a factor of e4y = 1.82 by this large distortion.
As a result the cross-over frequency, which is slightly higher than
the mean, is increased by a factor of about 1.12
but this change is expected for such a large distortion.
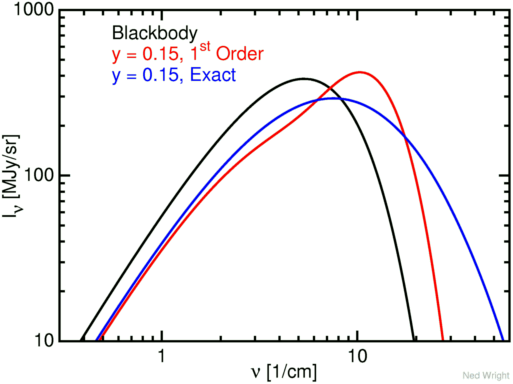
Since I got tired of seeing the weird red spectrum in too many talks,
I have generated the exact spectrum plot shown below.
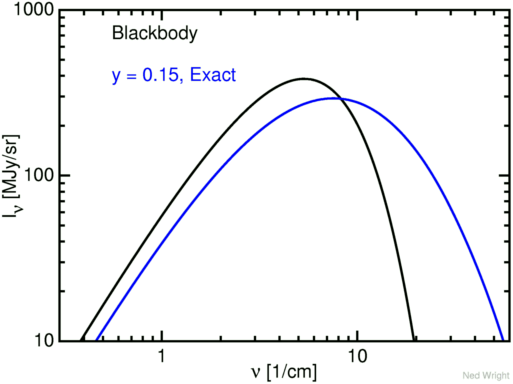
I hope that people speaking about the SZ effect and wanting a plot
showing both the blackbody and the distorted spectrum on a log-log
scale will use the figure above instead of some version of the old
inaccurate Figure 4 from S-Z (1980).
For real data from clusters, the values of y are much smaller.
A really big value of y = 0.0005 gives a distorted spectrum
that is hardly distinguishable from the blackbody on a log-log graph.
Therefore one typically plots the difference in intensity between the
on-cluster distorted spectrum and the off-cluster blackbody spectrum.
Such a plot is shown
below with both the exact and the first-order approximation:
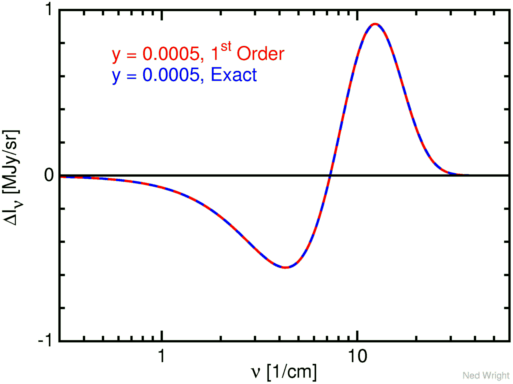
Clearly the first-order approximation is perfectly suitable for
analyzing real data, since the red and blue curves are very nearly
coincident for this value of y, and the first-order formula
will be even better for the more typical smaller values of y.
For reference, the first order spectrum is I = B+y*dI/dy with
dI/dy given by
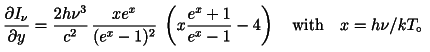
while the exact equation is based on convolving the input spectrum
with a Gaussian in log frequency space:
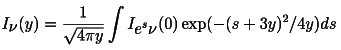
The plots included above were created using Postscript files that
evaluated these formulae, such as this
Postscript file for the second plot.
One can also worry about relativistic effects when the electron
temperature is high. The S-Z formulae are correct for
kT << mc2.
Wright (1979, ApJ, 232, 348) gives an exact numerical treatment
for a very hot plasma in the context of a hot intergalactic medium
that produces both the X-ray background and a distorted CMB spectrum.
This IGM model was ruled out by the COBE FIRAS data but the formulae
for computing the distortion are still correct.
Fabbri (1981, ApSS, 77, 529) was able to replace some of the
numerical integrations in Wright (1979) by analytic formulae.
Itoh and Nozawa (2004, A&A, 417, 827) provide tables
of the relativistic corrections and an accurate analytic fitting
formula.
These corrections are not too large for typical clusters with
kT < 15 keV.
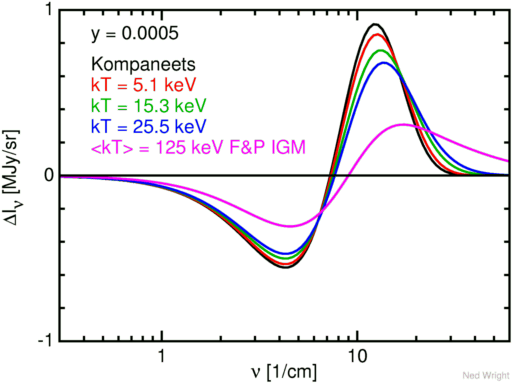
The figure above shows the change in intensity for y = 0.0005
for 4 conditions: the Kompaneets limit with kT/mc2
close to zero, and 3 curves with kT/mc2 of 0.01,
0.03 and 0.05 computed using the equations in
Wright (1979, ApJ, 232, 348). Also shown is curve for the
Field & Perrenod hot IGM model
considered by Wright (1979), which has an optical depth weighted mean
temperature of 125 keV.
Tutorial:
Part 1 |
Part 2 |
Part 3 |
Part 4
FAQ |
Age |
Distances |
Bibliography |
Relativity
© 2007-2008 Edward L.
Wright. Last modified 20 Jan2008