Arthur Stanley Eddington, in the last chapter of his 1926 book
The Internal Constitution of the Stars,
talks about Diffuse Matter in Space.
In the first page of this chapter, Eddington computes an effective
temperature of 3.18 K, but this has nothing to do with the
2.725 K
blackbody
spectrum of the
Cosmic Microwave Background (CMB).
Here is a quote of what Eddington actually said:
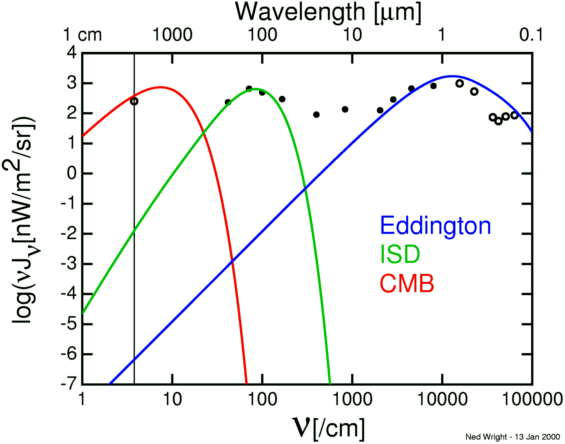
The total light received by us from the stars is estimated to be equivalent to about 1000 stars of the first magnitude. [...] We shall first calculate the energy density of this radiation. [...] Accordingly the total radiation of the stars has an energy density of [...] E = 7.67 10-13 erg/cm3. By the formula E = a T4 the effective temperature corresponding to this density is 3.18o absolute. [...] Radiation in interstellar space is about as far from thermodynamical equilibrium as it is possible to imagine, and although its density corresponds to 3.18o it is much richer in high-frequency constituents than equilibrium radiation of that temperature.Eddington then specifies a model for the spectrum of his estimate for the interstellar radiation field which is plotted in blue in the figure below.

The near equality of the energy densities of starlight (Eddington's blue
curve) and the CMB is just a coincidence. The starlight radiation field
is concentrated in galaxies like the Milky Way, which only occupy one
part per million of the volume of the Universe,
while the CMB fills the entire Universe.
The diagram below shows three galaxies and the photons they emit color-coded
red, green and blue.
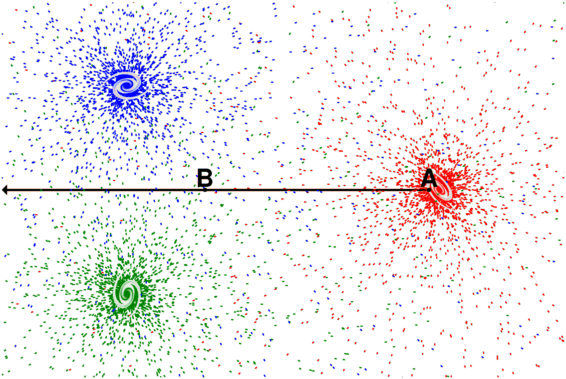
The density of radiation at position B would be relevant to the CMB if there were dust grains which could absorb this radiation and if these dust grains were able to radiate efficiently at the millimeter wavelengths of the CMB. We can estimate the radiation at B from our location at A if we carefully subtract out all the "red" photons to determine the Cosmic InfraRed [and optical] Background Radiation (CIBR). However,
Thus the effective temperature of the interstellar radiation in the Milky Way is irrelevant in cosmology and Eddington made no mention of it in his 1933 book, Expanding Universe. This book discusses Eddington's cosmological model, which starts out as the Einstein static model in which the repulsive cosmological constant just balances the gravitational attraction due to matter. But Eddington showed that this equilibrium was unstable, and the Einstein model would either collapse or start an unending expansion. Since the Universe was observed to be expanding, Eddington assumed that the initially static Universe fell out of equilibrium in the direction of expansion.
Back to Fads and Fallacies
Tutorial:
Part 1 |
Part 2 |
Part 3 |
Part 4
FAQ |
Age |
Distances |
Bibliography |
Relativity
© 2000-2006 Edward L. Wright. Last modified 23 Oct 2006