Relativity can be described using
space-time diagrams.
Contrary to popular
opinion,
Einstein
did not invent relativity.
Galileo
preceded him.
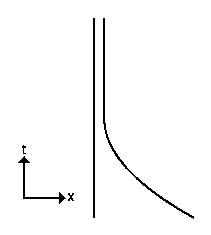
Aristotle had proposed that moving objects (on the Earth) had a natural
tendency to slow down and stop. This is shown in the space-time diagram
below.

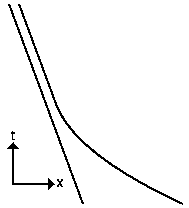
But Galilean transformations do not preserve velocity. Thus the statement "The speed limit is 70 mph" does not make sense -- but don't try this in court. According to relativity, this must be re-expressed as "The magnitude of the relative velocity between your car and the pavement must be less than 70 mph". Relative velocities are OK.
But 200 years after Newton the theory of electromagnetism was developed
into
Maxwell's equations. These equations describe waves with a speed
of 1/sqrt(epsilono*muo), where epsilono
is the constant describing the
strength of the electrostatic force in a vacuum, and muo
is the constant
describing the strength of the magnetic interaction in a vacuum. This is
an absolute velocity -- it is not relative to anything. The value of
the velocity was very close to the measured speed of light, and when
Hertz generated electromagnetic waves (microwaves) in his laboratory
and showed that they could be reflected and refracted just like light,
it became clear that light was just an example of electromagnetic
radiation. Einstein tried to fit the idea of an absolute speed of
light into Newtonian mechanics. He found that the transformation
from one reference frame to another had to affect the time -- the idea
of sliding a deck of cards had to be abandoned. This led to the
theory of special relativity. In special relativity, the
velocity of light is special. Anything moving at the speed of light
in one reference frame will move at the speed of light in all
unaccelerated reference frames. Other velocities are not preserved, so
you can still try to get lucky on speeding tickets.
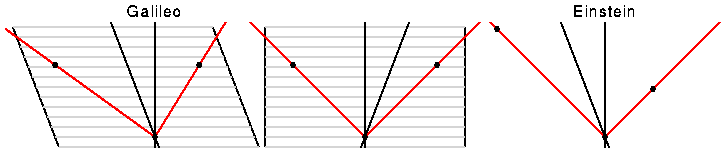
Thus in the situation shown in 3 space-time diagrams below, the central
section shows the worldline of one stationary observer, one observer moving
to the right, and two events on the future light cone on the event where the
two observers' worldlines cross.
What is the evidence for the invariance of the speed of light? The hypothesis
that the speed of light is c relative to its source can easily be disproved
by the one-way transmission of light from distant supernovae. When a star
explodes as a supernova, we see light coming from material with a large
range of velocities dv, at least 10,000 km/sec. Because of this range of
velocities, the spectral lines of a supernova are very broad due to the
Doppler shift. After traveling a distance D in time D/c, the arrival
time of the light would be spread out by dt = (dv/c)(D/c).
However, light could travel at speed c relative to a medium -- the ether.
If it did, then the rate of a "bouncing photon clock" moving with respect
to the ether
P(par) = L/(c-v) + L/(c+v) = [2L/c]/(1-v2/c2).If the clock is moving perpendicular to its axis, the light has to move a distance L sideways and a distance vt "upstream" to keep up with the clock, where t is the one-way time. The total distance traveled is ct, which is the hypotenuse of a right triangle with sides L and vt. Thus the period is given by:
(ct)2 = L2 + (vt)2 so t = L/sqrt(c2-v2) P(perp) = 2t = [2L/c]/sqrt(1-v2/c2).Thus the ether model predicts that
dP/P = [P(par)-P(perp)]/P = 0.5*v2/c2.Brillet and Hall (1979, PRL, 42, 549) actually built a bouncing photon clock (a laser stabilized to a Fabry-Perot etalon) on a rotating table and compared its rate to an atomic clock (a laser stabilized to a methane line).
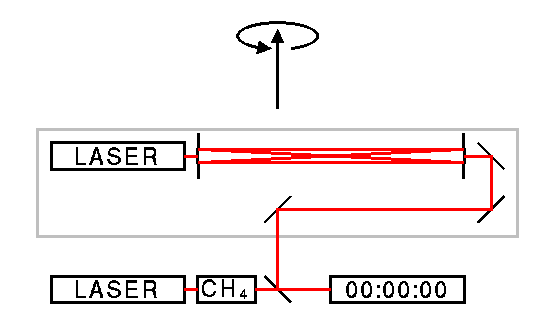
Michelson and Morley used two bouncing photon clocks at right angles to each other, but without the lasers and counters which didn't exist. This left an L-shaped interferometer. But they were able to show that dP/P was essentially zero instead of the ether model prediction.
The constancy of the speed of light allows the use of radar
(RAdio Detection And Ranging)
to measure the position and time of events not on an observer's
worldline. All that we need are a clock and the ability to emit and
detect radar pulses.
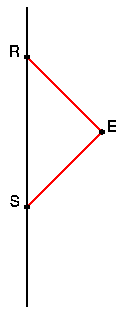
Armed with radar, we can determine the time of two events on the worldline
of an observer moving with respect to us. We can then compare the time
interval we measure to the time interval measured
by the moving observer. Consider the two observers A and B below.
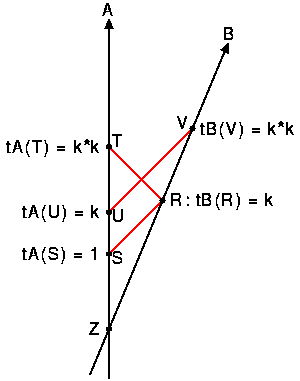
v = D/t = DA(R)/tA(R) = c(k*k-1)/(k*k+1).We can solve for k giving
k = sqrt((1+v/c)/(1-v/c))which is the relativistic Doppler shift formula. But we also find that tA(R) > tB(R), so A says that B's clock is running slow. The amount of this time dilation is
(1+k*k)/(2*k) = 1/sqrt(1-v2/c2).Thus moving clocks run slow. Note that B will also find that A's clock is running more slowly than his. There is a symmetric disagreement about clock rates. I have prepared an animation that toggles back and forth from the point-of-view of observer A to the point-of-view of observer B and illustrates the symmetry.
This slow down factor is exactly the slow down calculated above in the
ether model for a bouncing photon clock moving perpendicular to its
bounce axis. The clock moving parallel to the axis slows down by the
same amount under special relativity because of the
Lorentz-Fitzgerald contraction
of moving objects in the direction of motion.
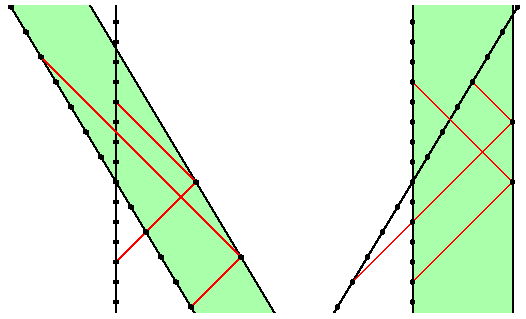
P(par) = [2L*sqrt(1-v2/c2)/c]/(1-v2/c2)
= [2L/c]/sqrt(1-v2/c2) = P(perp)
so the rate of a bouncing photon clock does not depend on the angle
between its velocity and its bouncing axis.
Because the clocks of different observers run at different rates, depending
on their velocities, the time for a given observer is a property of that
observer and his worldline. This time is called the proper time
because it is "owned" by a given particle, not because it is the "correct"
time. Proper time is invariant when changing reference frames because
it is the property of a particle, not of the reference frame or coordinate
system. In general, given any two events A and B with B inside the future
light cone of A, there is one unaccelerated worldline connecting A and B,
just as there is one straight line connecting two points in space. In the
frame of reference of the observer following this unaccelerated worldline,
his clock is always stationary, while clocks following any other worldline
from A to B will be moving at least some of the time. Because moving clocks
run slow, these observers will measure a smaller proper time between events
A and B than the unaccelerated observer.
Thus the straight worldline
between two events has the largest proper time, and all other curved
worldlines connecting the two events
have smaller proper times. This is exactly analogous to the fact that the
straight line between two points has the smallest length of all possible
curves between the points. Thus the "twin paradox" is no more paradoxical
than the statement that a man who drives straight from LA to Las Vegas
will cover fewer miles than a man who drives from LA to Las Vegas via Reno.
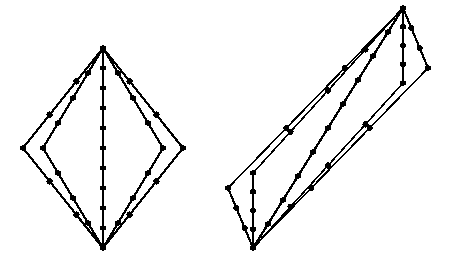
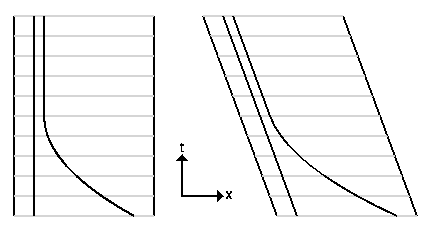
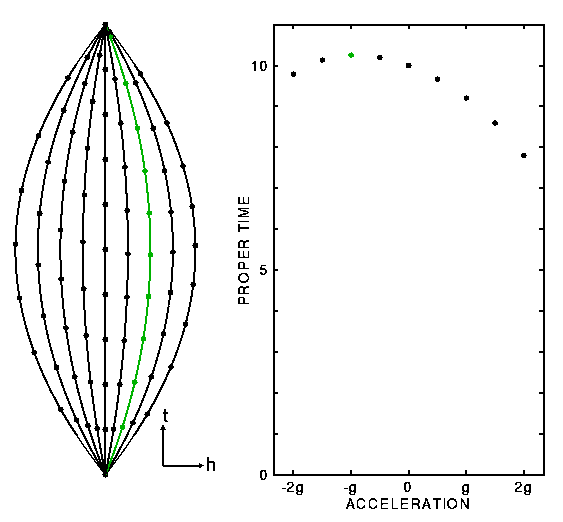
The pair of space-time diagrams above show quintuplets separated at birth.
The middle worldline shows the quint who stays home.
The space-time diagram on the left is done from the
point of view of the middle quint.
Each dot on a
worldline is a birthday party, so the middle quint is 10 years old when
they all rejoin each other, while the other quints are 6 and 8 years old.
The space-time diagram on the right shows the same events from the
point of view of an observer initially moving with one of the moving
quints. When the quints come together their ages are still 6, 8, 10,
8, and 6 years. Thus the straight worldline between two events can
be found by maximizing the proper time, just as the straight line
between two points can be found by minimizing the length.
Now we come to a matter of gravity: how can gravity be an inverse square
law force, when the distance between two objects can not even be defined
in Einstein's special relativity? Special relativity was constructed
to satisfy Maxwell's equations, which replaced the inverse square law
electrostatic force by a set of equations describing the electromagnetic
field. So gravity was the only remaining action-at-a-distance
inverse square law force.
And gravity has a unique property; the acceleration due to gravity at
a given place and time is independent of the nature of the body.
Thus through
any event in space-time, in any given direction, there is
only one worldline corresponding to motion solely influenced by gravity.
Compare this to the geometric fact that through any point, in any given
direction, there is only one straight line. We are led to propose that
worldlines influenced only by gravity are really straight worldlines.
But how can an accelerating body have a straight worldline?
It all depends on how you measure it.
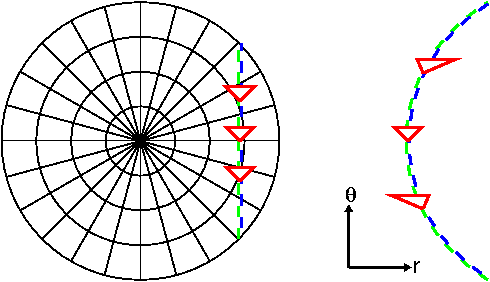
Suppose we plot a straight line on polar graph paper, and then
make a plot of radius vs angle as shown below?
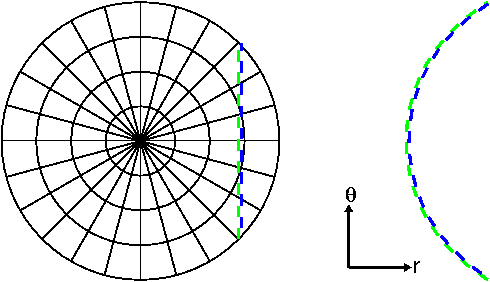
Einstein proposed that the effects of gravity (in a small region of
spacetime) are equivalent to the effect of using an accelerated frame
of reference without gravity. As as example, consider the famous
"Einstein elevator" thought experiment. If an elevator far out in space
accelerates upward at 10 meters/second2,
it will feel like a downward
acceleration of gravity at 1 g = 10 m/s2.
If a clock on the ceiling of
the elevator emits flashes of light f times per second, an observer on
the floor will see them arriving faster than f times per second because
of the Doppler shift due to the acceleration of the elevator during the
light transit time.
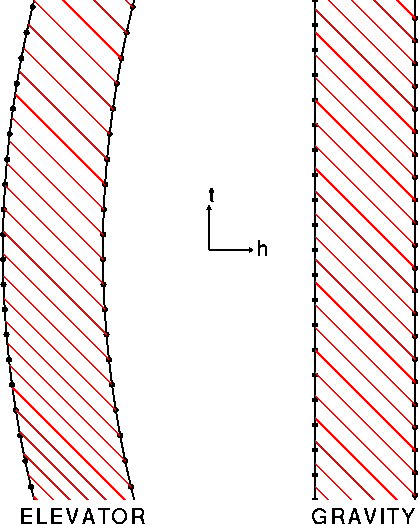
The effect of gravity on clocks was tested to greater precision by Vessot etal (1980, PRL, 45, 2081) who launched a hydrogen maser straight up at 8.5 km/sec, and watched its frequency change as it coasted up to 10,000 km altitude and then fell back to Earth. The frequency shift due to gravity was (f'/f -1) = 4*10-10 at 10,000 km altitude, and the experimental result agreed to within 70 parts per million of this shift.
Because of the gravitational speedup for uphill clocks,
an observer moving between two events
can achieve a larger proper time by shifting his worldline upward in the
middle. Going too far upward requires moving so fast that time dilation
due to motion reduces the proper time more than the gravitational speedup,
so there is an optimum curvature to the worldline that maximizes the
proper time.
Curved coordinates alone, such as the polar graph, do not provide
a satisfactory model for gravity. Two straight lines through the same
point but with different directions will never cross again, while two
worldlines influenced only by gravity which pass through the same event
with different velocities can cross again. Consider the Galileo
spacecraft, which made two Earth flybys. In between the flybys,
Galileo was on an elliptical orbit with a 2 year period. In order
to allow "straight" lines to cross multiple times, a curved space-time
is needed. As a familiar example of a curved space, consider the
surface of the Earth and the great circle arc connecting two cities.
The great circle is the shortest distance between two points on the
surface of the Earth, and it is the path followed by airliners.
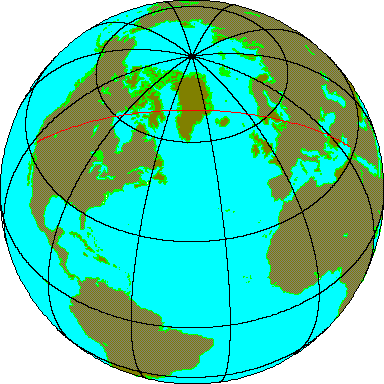
Plotting latitude vs longitude, as if longitude were time and latitude
position, gives the pseudo-spacetime diagram below.
Einstein was able to compute the perihelion advance of Mercury using general relativity, and his calculation matched an observed discrepancy with Newtonian predictions. Einstein also computed that light passing by the Sun would be deflected by twice as much as a prediction using Newtonian gravity and Newton's particle model for light would suggest. The same effect causes a delay of light passing by the limb of the Sun, known as the Shapiro delay, which has now been measured to great accuracy and agrees with the prediction of general relativity.
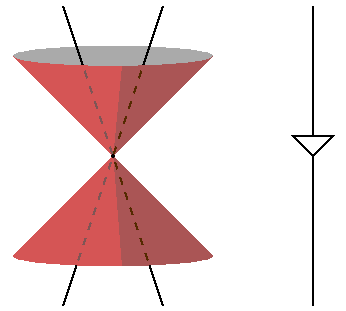
Unlike the restricted set of Lorentz transformations allowed in
special relativity, the more
general coordinate transformations of general relativity will change
the slope of the walls of the lightcones. In other words, the
speed of light (dx/dt) will change in the transformed coordinates:
dx'/dt' will not equal dx/dt in general. The light cones can tilt
or stretch. The figure below shows "lightcones" added to the
radius vs angle example given above:
Thus the fundamentals of relativity that are important for cosmology are:
Relativity also leads to interesting objects such as black holes, but these are not very relevant to cosmology.
There are many books on relativity available, but two that stick to a simple level of mathematics are:
Cosmology Tutorial:
Part 1 |
Part 2 |
Part 3 |
Part 4
Cosmology FAQ |
Age |
Distances |
Bibliography |
Relativity
© 1996-2022 Edward L. Wright. Last modified 30 Mar 2022