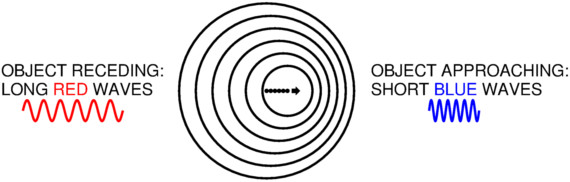
Light from moving objects will appear to have different wavelengths
depending on the relative motion of the source and the observer.

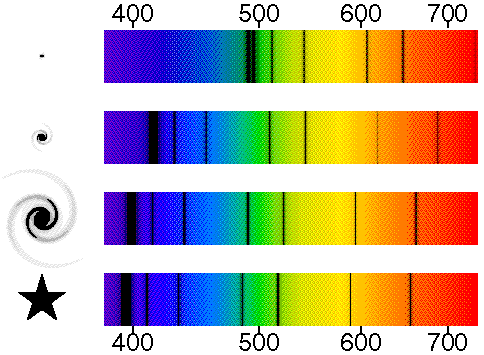
The schematic diagram below shows a galactic star at the bottom left with
its spectrum on the bottom right.
The spectrum shows the dark absorption lines first seen by Fraunhofer.
These lines can be used to identify the chemical elements in distant
stars, but they also tell us the radial velocity.
The other three spectra and pictures from bottom to top show a nearby
galaxy, a medium distance galaxy, and a distant galaxy.
The pictures on the left are negatives, of course, so the brightest
parts of the galaxies are black. Notice how
the pattern of absorption lines shifts to the red as the galaxies get
fainter.
The numbers above and below the spectra are the measured wavelengths
in nm [nanometers].
lambda(observed)
1+z = ----------------
lambda(emitted)
which is
397 401 414 438 491 523 595 663
1+z = --- = --- = --- = --- = --- = --- = --- = --- = 1.01
393 397 410 434 486 518 589 656
in this case so z = 0.01 for the bright galaxy. The radial velocity is usually
approximated by v(rad) = cz, where c is the speed of light,
The medium bright galaxy is moving away
at 15,000 km/sec with z = 0.05, while the faintest and most distant galaxy is
moving away at 75,000 km/sec with z = 0.25.
When z is larger than 1 then cz is faster than the speed of light and,
while recession velocities faster than light are allowed, this
approximation using cz as the recession velocity of an object is no longer
valid. Thus for the largest known redshift of z=6.3, the recession velocity
is not 6.3*c = 1,890,000 km/sec.
It is also not the 285,254 km/sec given by the special relativistic Doppler
formula 1+z = sqrt((1+v/c)/(1-v/c)).
The actual recession velocity for this object
depends on the cosmological parameters, but for an OmegaM=0.3
vacuum-dominated flat model the velocity is 585,611 km/sec.
This is faster than light.
© 1996-2002 Edward L. Wright. Last modified 23-Feb-2002