Formation of a Black Hole
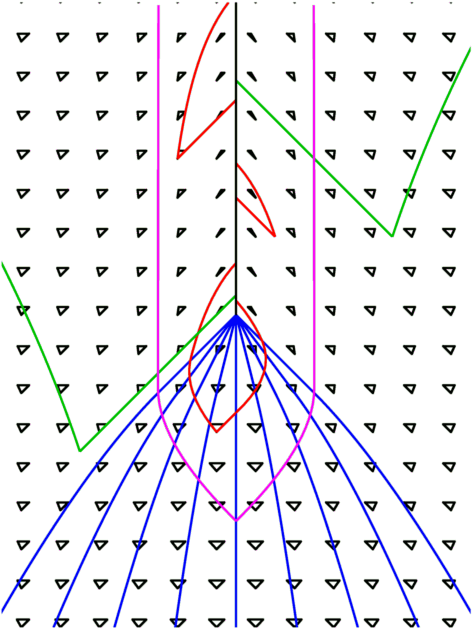 The space-time diagram at right shows matter in blue
collapsing to form a singularity [the solid black line],
while the green curves are the future lightcones from
events where light can escape to infinity, while the red
curves are future lightcones from events where light cannot
escape. The boundary between these two regions in space-time
is the magenta curve. This boundary of the trapped region is
the event horizon of the black hole. Note that the
event horizon forms before the singularity and entirely
surrounds it, so there is not a naked singularity
in this space-time. The cosmic censorship hypothesis
states that this is always true, but this hypothesis appears to
be false in general, even though it is correct for this space-time
and for all (or almost all) physically plausible space-times.
The space-time diagram at right shows matter in blue
collapsing to form a singularity [the solid black line],
while the green curves are the future lightcones from
events where light can escape to infinity, while the red
curves are future lightcones from events where light cannot
escape. The boundary between these two regions in space-time
is the magenta curve. This boundary of the trapped region is
the event horizon of the black hole. Note that the
event horizon forms before the singularity and entirely
surrounds it, so there is not a naked singularity
in this space-time. The cosmic censorship hypothesis
states that this is always true, but this hypothesis appears to
be false in general, even though it is correct for this space-time
and for all (or almost all) physically plausible space-times.
The little black triangles in the diagram are the local lightcones,
and they trace out the metric structure of this space-time. The
coordinates used in this diagram are the Kerr metric coordinates
for times later than the creation of the singularity.
The Kerr metric describes a rotating black hole, but the rotation
is set to zero here.
Before the creation of the singularity a simple analytic form is used
instead of the exact solution for a collapsing sphere of pressureless
matter.
Space-time is strongly curved near a black hole, so one has to be
very careful about definitions. In particular, the radius of a black
hole can not be defined as the distance from the central singularity to
the event horizon, because observers trying to measure this would inevitably
fall into the singularity. But if one measures the circumference of the
event horizon and divides by 2*pi, one gets RS = 2GM/c2,
which is called the
Schwarzschild radius. Numerically it is 3 km for a
1 solar mass object. This is only a factor of a few smaller than the radius
of a neutron star, which is 10 km for a 1.4 solar mass object.
Tutorial:
Part 1 |
Part 2 |
Part 3 |
Part 4
FAQ |
Age |
Distances |
Bibliography |
Relativity
© 2005 Edward L.
Wright. Last modified 7 Jan 2005
 The space-time diagram at right shows matter in blue
collapsing to form a singularity [the solid black line],
while the green curves are the future lightcones from
events where light can escape to infinity, while the red
curves are future lightcones from events where light cannot
escape. The boundary between these two regions in space-time
is the magenta curve. This boundary of the trapped region is
the event horizon of the black hole. Note that the
event horizon forms before the singularity and entirely
surrounds it, so there is not a naked singularity
in this space-time. The cosmic censorship hypothesis
states that this is always true, but this hypothesis appears to
be false in general, even though it is correct for this space-time
and for all (or almost all) physically plausible space-times.
The space-time diagram at right shows matter in blue
collapsing to form a singularity [the solid black line],
while the green curves are the future lightcones from
events where light can escape to infinity, while the red
curves are future lightcones from events where light cannot
escape. The boundary between these two regions in space-time
is the magenta curve. This boundary of the trapped region is
the event horizon of the black hole. Note that the
event horizon forms before the singularity and entirely
surrounds it, so there is not a naked singularity
in this space-time. The cosmic censorship hypothesis
states that this is always true, but this hypothesis appears to
be false in general, even though it is correct for this space-time
and for all (or almost all) physically plausible space-times.