Moment of Inertia
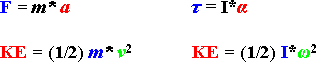
Moment of Inertia
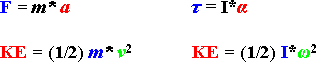
Above are four formulas two for linear motion, and two for rotational. The
first is another way to calculate torque. As you can see it is very much like
the formula for force. The second is the kinetic energy formula and it is also
very similar to its linear counterpart. The new term in these formulas is I,
which stands in the place of mass in the linear equation. This is the moment
of inertia. The thing with rotational motion is that the position relative to
the axis of rotation is very important, as you already saw from tangential equations
and the torque equation. That is why not only mass but its distribution must
be taken into account.




As you can see in the animations, of the rolling objects the third one which
has almost all the mass near the center, gets to the bottom faster, and the
hoop which has all of its mass far from the center is by far the slowest. This
is due to the fact that is has the highest moment of inertia (![]() )
and as a result it is hart to make it rotate. The uniform cylinder is easier
to turn with a moment:
)
and as a result it is hart to make it rotate. The uniform cylinder is easier
to turn with a moment: ![]() , and the
third object which has almost all mass near the center, and this a moment
, and the
third object which has almost all mass near the center, and this a moment ![]() is very easy to turn. But what of the box which as you can see got to the bottom
faster? The answer is simple: it takes energy to make things turn. The potential
energy of the box is spent solely on moving down linearly. On the other hand
the other three objects have to move down linearly and roll, as a result
they lose to the box. Note however that this is only the case when the box does
not experience friction. The rolling objects on the other hand need friction
for them to roll.
is very easy to turn. But what of the box which as you can see got to the bottom
faster? The answer is simple: it takes energy to make things turn. The potential
energy of the box is spent solely on moving down linearly. On the other hand
the other three objects have to move down linearly and roll, as a result
they lose to the box. Note however that this is only the case when the box does
not experience friction. The rolling objects on the other hand need friction
for them to roll.
For point mass objects need to use this formula to calculate the moment of inertia:
![]() [moment of inertia] = [mass] [distance
to axis of rotation squared]
[moment of inertia] = [mass] [distance
to axis of rotation squared]
If you have several point masses in a system you just add them all up.
For uniform distributions of mass integrals must be taken to find the moment
of inertia, but for common objects such as spheres cylinders and rods the formulas
to use have been calculated and are given in the book.