The first thing you need to know about rotational motion are the three basic measurements. There is theta which measures the angle, omega which measures the angular speed, and alpha which measures the angular acceleration. If you also want to know the distances and another three measurements which deal with arc length are used.

- Theta - the angle

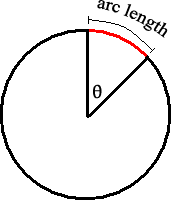
In the picture of the circle above you can see the theta and the arc length. In this case the theta happens to be 45 degrees or (PI/4) radians depending on which measurement system you use. The arc length is calculated from a simple formula: [arc length]=[radius]*[angle in radians]
So if the radius is 16 units the arc length is (PI/4)*16= 4PI

- Omega - the angular velocity

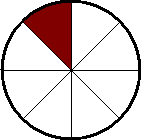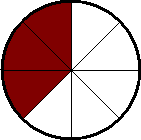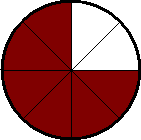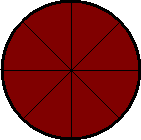
The animation above is an example of angular speed. Each of those sections is 45 degrees or PI/4 radians and each is covered in .75 seconds.
So by the formula [average angular velocity]=[change in angle] / [change in time] you get (PI/4)/.75=(1/3)PI per second. This is however only average velocity which takes the start and end points of the motion and calculates the velocity from that. There is also instantaneous velocity: . This formula measures the velocity at any instant in time during the motion. .

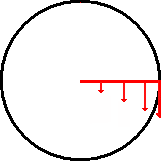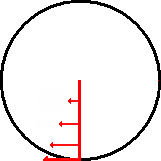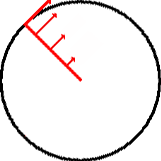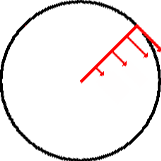
The concept of tangential velocity is based on the fact that if you were to suddenly release the rotating object from its orbit it would fly off at a tangent to the point where it was when the release happened. Thus the arrows indicate in which direction the object would fly off at that point in the rotation. Note also that as you get closer to the center the arrows get smaller. This is due to the fact that tangential velocity is related the radius. The smaller the radius the smaller the tangential velocity. The formula is simple: [tangential velocity]=[radius]*[angular velocity]
So in this example (R being 10) 10*PI/2=5PI m/s

- Alpha - the angular acceleration

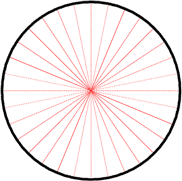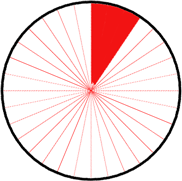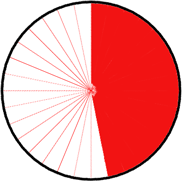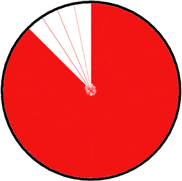
In this animation the circle is divided into slices which are PI/16 radians (11.25degrees) each. Were this a constant angular velocity one slice would be covered per second. But there is an acceleration of PI/16 /sec/sec present. Thus first one slice is covered, then two then three and so on. The calculation is also quite simple and analogous to regular acceleration.
The formula is: [average angular acceleration]=[change in angular velocity]/[time]
So in the case of the animation: (PI/8 per sec – PI/16 per sec) / 1 sec = (PI/16)/sec/sec.

As with velocity this is average acceleration that is calculated from the start and end velocities. The instantaneous acceleration is denoted by: where dt is a instant of time during the trip.

Tangential acceleration is also quite easy to figure out. The formula is quite similar to the previous: [tangential acceleration]=[radius]*[angular acceleration]

Remember: never use degrees in these formulas, they only work with radians.